
# This loop iterates over the unsorted items for j in range(i + 1, len(nums)): # We assume that the first item of the unsorted segment is the smallest Implementation def selection_sort( nums): # This value of i corresponds to how many values were sorted for i in range( len(nums)): This reiterates until the last item of the list is the remaining element to be examined. Now we know that the first element of the list is sorted, we get the smallest element of the remaining items and swap it with the second element. We then search the entire list for the smallest element, and swap it with the first element. In practice, we don't need to create a new list for the sorted elements, what we do is treat the leftmost part of the list as the sorted segment. We continuously remove the smallest element of the unsorted segment of the list and append it to the sorted segment. This algorithm segments the list into two parts: sorted and unsorted. Therefore, if we have n elements in our list, we would have n iterations per item - thus Bubble Sort's time complexity is O(n^2). Our swapped flag would be set to True on every iteration. In the worst case scenario (when the list is in reverse order), this algorithm would have to swap every single item of the array. We set swapped to True in the beginning to ensure that the algorithm runs at least once. The algorithm runs in a while loop, only breaking when no items are swapped. # Set the flag to True so we'll loop again Swapped = False for i in range( len(nums) - 1): With the optimization, we can implement Bubble Sort in Python as follows: def bubble_sort( nums): # We set swapped to True so the loop looks runs at least once If you'd like to read a more detailed, dedicated article on Bubble Sort, we've got you covered! Implementation If no swaps occurred, the flag would remain False and the algorithm will stop. So, whenever we swap values we set a flag to True to repeat sorting process. How would we know that we're finished sorting? If the items were in order then we would not have to swap any.

Obviously, to optimize the algorithm, we need to stop it when it's finished sorting, otherwise it'll reevaluate an already sorted array many times. What if only a single swap needs to be made in the array? Why would we still iterate though it n^2 times, even though it's already sorted? Upon reaching the end of the list, it repeats this process for every item. This process continues to the last pair of items in the list. We then move to the next pair of elements, compare their values and swap as necessary.

If they are already in order we leave them as is. If the first element is larger than the second element, we swap them. We begin by comparing the first two elements of the list. This simple sorting algorithm iterates over a list, comparing elements in pairs and swapping them until the larger elements "bubble up" to the end of the list, and the smaller elements stay at the "bottom".
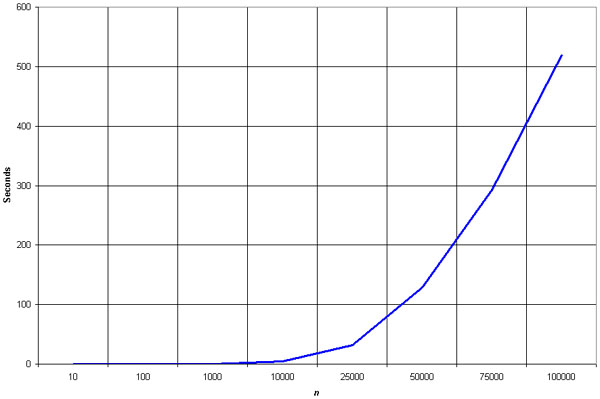
Selection sort vs bubble sort runtime free#
Of course, you're free to adapt them to your need. We'll also compare how quickly they sort items in a list.įor simplicity, algorithm implementations would be sorting lists of numbers in ascending order.
Selection sort vs bubble sort runtime code#
In this article we'll have a look at popular sorting algorithms, understand how they work and code them in Python. Over the years, computer scientists have created many sorting algorithms to organize data. We may have to rearrange the data to correctly process it or efficiently use it. Sometimes, data we store or retrieve in an application can have little or no order.


 0 kommentar(er)
0 kommentar(er)
